ESCALAS ESCALAS
ESCALAS ESCALAS
 TEMA 9 TEMA 9
TEMA 9 TEMA 9
VOLUMEN Y CAPACIDAD
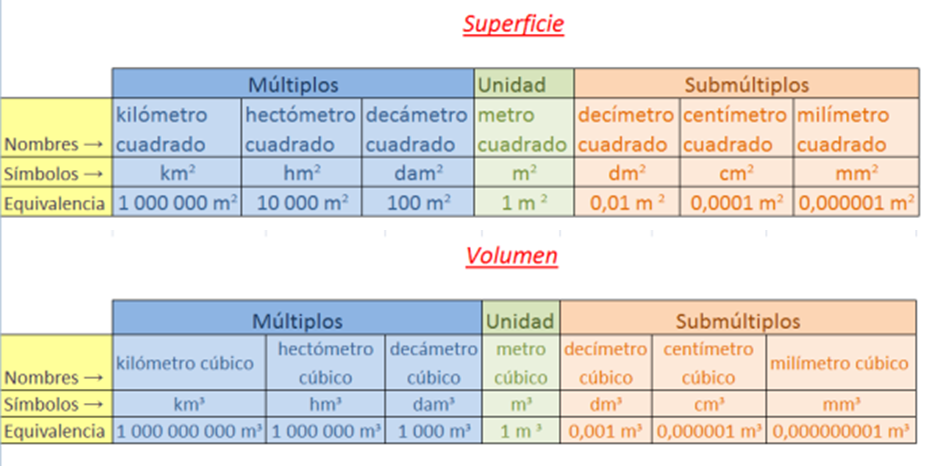
SUPERFICIE Y VOLUMEN
UNIDADES DE LONGITUD, MASA Y VOLUMEN.
 TEMA 8 TEMA 8
TEMA 8 TEMA 8
PROPORCIONALIDAD Y REGLA DE TRES
Os dejamos por aquí un vídeo explicativo de la regla de tres en problemas de proporcionalidad, para que lo podáis ver las veces que queráis y aclarar dudas.
PORCENTAJES
PROPORCIONALIDAD
La proporcionalidad es la relación que tienen dos magnitudes. Fijaos en este ejemplo
En una caja hay 3 plátanos. Por lo tanto, en 2 cajas habrá 6; en 3, 9 plátanos, y así sucesivamente.
Crece de forma proporcional siempre multiplicando por 3.
Por lo tanto, son magnitudes proporcionales.
Aquí tenéis unas actividades para practicar con este concepto.
 TEMA 6 TEMA 6
TEMA 6 TEMA 6
APROXIMACIONES Y ESTIMACIONES DE NÚMEROS DECIMALES
Aquí os dejamos ejercicios para practicar las aproximaciones de los números decimales.
OPERACIONES CON NÚMEROS DECIMALES
 TEMA 5 TEMA 5
TEMA 5 TEMA 5
NÚMEROS MIXTOS
En el siguiente vídeo, podéis repasar cómo pasar de fracción a número mixto. De nuevo Susi, os muestra varios métodos como los que hemos visto en clase.
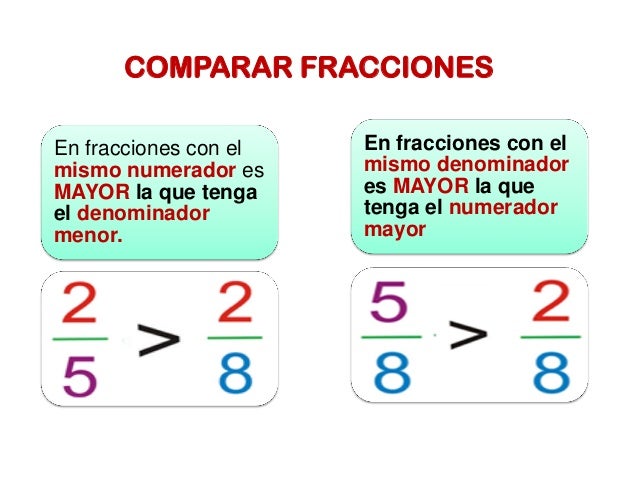
FRACCIONES EQUIVALENTES
Aquí os dejamos de nuevo a las profe Susi con una explicación de lo que son las fracciones equivalentes y cómo calcularlas.
Ahora podéis poner en práctica todo lo que hemos aprendido sobre las fracciones equivalentes. ¡Adelante!
 TEMA 4 TEMA 4
TEMA 4 TEMA 4
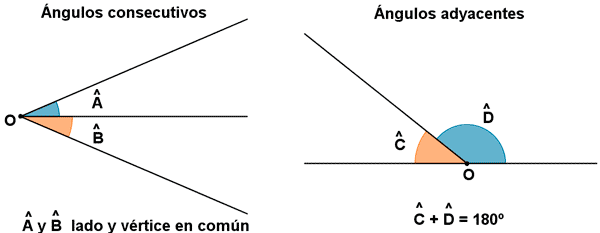
SUMAS Y RESTAS DE ÁNGULOS
En estos vídeos tenéis a las profe Susi que explica cómo se opera con los ángulos.
En la actividad de abajo también incluye otros vídeos, pero son más largos. No es necesario que los veáis. Simplemente, coged papel y lápiz y a practicar con la suma y resta de ángulos.
UNIDADES DEL SISTEMA SEXAGESIMAL
El sistema sexagesimal es el que usamos para medir ángulos, que es lo que hemos aprendido en este tema.
Teniendo en cuenta estos cambios de unidades que tenéis arriba, os dejamos por aquí algunas actividades para practicar.
CAMBIO UNIDADES SISTEMA SEXAGESIMAL
 TEMA 3 TEMA 3
TEMA 3 TEMA 3
 TEMA 2 TEMA 2
TEMA 2 TEMA 2
MÍNIMO COMÚN MÚLTIPLO Y MÁXIMO COMÚN DIVISOR
Hemos aprendido en este tema a calcular el mínimo común múltiplo (mcm) y el máximo común divisor (mcd).

Lo que más nos cuesta es saber cómo aplicarlo en la resolución de problemas.
Os dejamos aquí un vídeo de una profesora que nos gusta mucho y que explica más trucos de los vistos en clase para saber diferenciar lo que nos piden en los problemas.
Os dejamos por aquí actividades para que practiquéis.
MÚLTIPLOS Y DIVISORES
 TEMA 1 TEMA 1
TEMA 1 TEMA 1
POTENCIAS DE BASE 10
POTENCIAS

A continuación tenéis unas cuantas actividades para poner en práctica lo aprendido.
OPERACIONES COMBINADAS
Comenzamos este curso viendo de nuevo las operaciones combinadas. Es decir, cuando nos encontramos diferentes operaciones juntas.
Recordad que lo importante es mantener el orden o jerarquía a la hora de resolverlas.

Poner en práctica este orden con las siguientes actividades y juegos que os dejamos por aquí.
 TEMA 1 TEMA 1
TEMA 1 TEMA 1
 MATEMÁTICAS MATEMÁTICAS
MATEMÁTICAS MATEMÁTICAS
CIRCUNFERENCIAS Y CÍRCULOS
TRIÁNGULOS Y POLÍGONO REGULARES
Aquí tenéis unas cuantas actividades para trabajar con lo aprendido sobre los triángulos y los polígonos regulares.
LOS POLÍGONOS
Comenzamos un tema nuevo de matemáticas y preparamos nuestras reglas, transportadores y compases para dibujar polígonos.
Por aquí os dejamos unas cuantas actividades para repasar.
OPERACIONES CON DECIMALES

¿Cómo lleváis las operaciones con decimales? Os dejamos unos cuantos recursos para repasar:
En estos dos primeros enlaces, tienes vídeos para repasar y ejercicios sobre operaciones con la unidad seguida de ceros (10, 100, 1000...)
Vídeos y operaciones con la unidad seguida de ceros
Multiplicación y división de la unidad seguida de ceros
Ahora saca una hoja para realizar tus operaciones y comprobar cómo te ha salido:
Divisiones con decimales fáciles
Juegos con decimales:
https://www.cokitos.com/parejas-de-fracciones-y-decimales/play/
https://www.cokitos.com/numeros-decimales-con-el-hamster/play/
Y ahora, un juego-reto. Intenta resolver la siguiente pirámide de decimales:
SUMA Y RESTA DE FRACCIONES
Estamos trabajando las sumas y restas de fracciones. Las de igual denominador las tenemos dominadas. Aún así, os dejamos algunas fichas para que las repaséis:
Operaciones combinadas de fracciones

Las que nos están costando un poco más son las de distinto denominador. Como os hemos explicado en clase, hay que buscar una fracción equivalente a las dadas que compartan denominador. Para ello, buscamos el primer múltiplo común a ambos denominadores.
Si buscáis encontraréis otros métodos, que lo explican con la "receta" para operar, pero lo importante es que entendáis lo que estáis haciendo.

Vamos a practicar. No olvidéis papel y boli para buscar el primer múltiplo común a los denominadores.
FRACCIONES EQUIVALENTES
¿Cómo lleváis las fracciones equivalentes? Aquí un pequeño vídeo de repaso:
Ahora comprobad lo que habéis aprendido en estas actividades:
Aquí una ficha nivel principiante:
Calcula la fracción equivalente
Un poco más:
FRACCIONES PROPIAS E IMPROPIAS. NÚMEROS MIXTOS
OPERACIONES COMBINADAS

Pon a prueba tus conocimientos con las siguientes actividades:
OPERACIONES COMBINADAS (NIVEL FÁCIL)
DIVISIONES DE DOS CIFRAS
Vamos con la práctica de la división. Para empezar, aquí tenéis un vídeo explicativo que sigue la misma estructura trabajada en clase:
¿Te animas a jugar? En este juego debes estimar el resultado, puedes ayudarte de un papel si te hace falta, ¡pero tienes que ser rápido!
POTENCIAS
NÚMEROS ROMANOS
LOS NÚMEROS ROMANOS

Aquí tenéis un breve video explicativo del origen de estos números.
Y a continuación unas actividades para practicar.
PRACTICA CON LOS NÚMEROS ROMANOS
PRACTICA MÁS CON LOS NÚMEROS ROMANOS
VALOR POSICIONAL DE LOS NÚMEROS
Los números naturales pueden estar formados por una o varias cifras. Cada número tiene un valor diferente dependiendo del lugar que ocupa. Aquí tenéis un ejemplo:
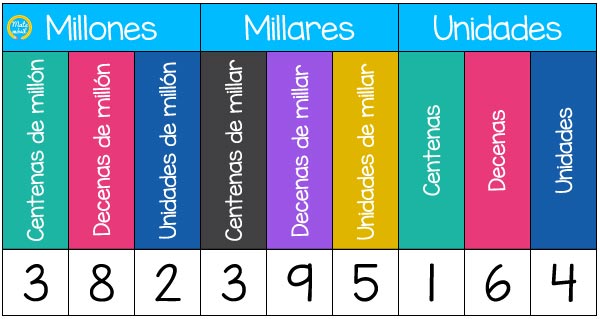
En el número 382.395.164, la cifra 5 ocupa las unidades de millar y equivale a 5.000.
Si lo descomponemos quedaría de la siguiente manera:
382.395.165 = 300.000.000 + 80.000.000 + 2.000.000 + 300.000 + 90.000 + 5.000 + 100 + 60 + 5
o
382.395.165 = 3Cmillón + 8Dmillón + 2Umillón + 3C millar + 9D millar + 5U millar + 1C + 6D + 5U
Ahora os toca a vosotros poneros a practicar. Para ello, pinchad en los siguientes enlaces.
VALOR POSICIONAL DE LOS NÚMEROS (FÁCIL)
VALOR POSICIONAL DE LOS NÚMEROS (DIFÍCIL)
 THAT QUIZ THAT QUIZ
THAT QUIZ THAT QUIZ
THATQUIZ
Cómo nos está gustando esta página para practicar el cálculo mental. Aquí os iremos dejando los enlaces para que vayáis haciendo las pruebas que os vayamos diciendo. ¡A mejorar vuestras marcas!
5º A
5ºB
https://www.thatquiz.org/es/classpage?0361568abcdc179
https://www.thatquiz.org/es/classpage?03601278defc17e
5ºC